SigmaPro Blog
SigmaPro is a leading global provider of Lean Six Sigma Training, Lean Six Sigma consulting and business improvement programmes designed to help organisations achieve breakthrough performance improvement.
Understanding Basic Statistics
- Font size: Larger Smaller
- Hits: 155025
- 0 Comments
- Subscribe to this entry
- Bookmark
Why Statistics?
When we run an improvement project, we will be collecting data. Take as an example a project to reduce scrap on an assembly line, or a project to improve throughput time on processing an insurance claim. In both cases we will have questions such as which are the biggest problems, what is the current performance of the process, how variable is it? We must collect and use data to answer these questions. Once collected, turning data into meaningful information is essential to our project.
Once we have collected data and analysed it, and hopefully made some improvements, we will then have further questions such as has my process performance improved, have we made a difference, or is in fact the process performance worse?
Lean Six Sigma is a data driven decision making approach. An understanding of data, and how to turn data into meaningful information, is a key skill for any lean Six Sigma practitioner. Statistics are used in all phases of a Lean Six Sigma project, but are particularly important in the Measure, Analyse and Improve phase.
Data Types
There are two basic types of data, continuous and categorical.
- Continuous data can take upon infinite number of real values. Examples of continuous variables are weight, age, distance, or time. For example, a weight of a person can be anywhere on a continuum from 140 to 230 pounds.
- Categorical data is where data falls into categories, such as colours (green, red, blue) or days of the week. With categorical data we must put the item in question into a “bucket”. We can’t be half in Monday and half in Tuesday, it’s either Monday or Tuesday!
The type of data is important because the calculations involved finding parameters for each type are different.
Continuous Data
There are some basic principles which apply to any continuous variable.
- Variation always exists. If we have a process producing a shaft, a surgeon performing an operation, a clerk processing an invoice or indeed any other process there will be variation. The shafts produced will have different diameters, the surgeon’s times will be different, and the clerks processing times will vary. Variation will always exist. Some people will argue that their processes do not vary, but in fact all processes vary, some more than others. If the variation is small it may be difficult to detect but there will be variation.
- Assuming we have an adequate measurement system, then the variation can be measured and the results plotted. If we count the number of shafts produced within certain size groupings then we can plot the number in each group on a chart.
- The chart we produce will at first look like random groupings, with one or two shafts showing in each group. The graphs is called a histogram, and as we measure more and more shafts we will start to see a pattern emerge, the shape of the histogram will start to look like a bell, it is called a distribution.
Descriptive Statistics
Distributions can be described by certain characteristics or parameters, the parameters describe the central location, spread (dispersion) and symmetry of the distribution.
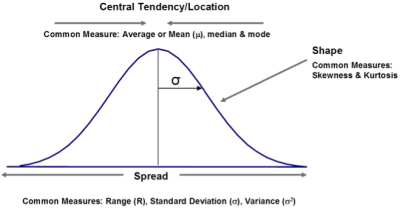
There are three parameters to describe the central location of a distribution; these are mean, median and mode.
- Mean is the average of a set of values. Found by adding up all the numbers in the data and dividing by the number of values you have. It is the measure of location for normal data but can be influenced by outliers or skewed data.
- Median is the midpoint in a string of sorted data, where 50% of the values are below it and 50% are above. It is the best measure of location for skewed data.
- Mode is the most frequently occurring value. It is particularly useful for attribute data.
Spread can be measured by range, which is the difference between the largest and the smallest observations, its purpose is to measure the dispersion between the highest and lowest values of a data set. The advantage of range is that it is easy to calculate and easy to understand. What are some of the disadvantages?
Range has limited value as a parameter to describe spread and shape of a distribution because it does not consider the shape of the distribution. Another parameter which can be used to measure spread is called variance.
Variance measures how far a set of numbers is spread out. A variance of zero indicates that all the values are identical. Variance is always non-negative: a small variance indicates that the data points tend to be very close to the mean and hence to each other, while a high variance indicates that the data points are very spread out around the mean and from each other. The way to calculate variance is to take each data point and subtract the mean value from it. Square the result obtained so that the data does not end up being zero if the mean is zero. Add up all the calculated values and divide by the number of data points.
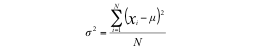
An example would be of we have 10 people in a room and we record their heights in metres with the following results:
1.67, 1.68, 1.55, 1.45, 1.45, 1.67, 1.26, 1.42, 1.61, 1.53
To calculate the variance, first find the average by adding up all the numbers and dividing by 10. (The answer is 1.53). Then take each height reading, subtract the mean and square the result. For example:
(1.67-1.53) * (1.67-1.53) = 0.14 * 0.14 = 0.0199
Do this for all values and add them all up, this gives 0.166
Divide by the number of values (10) gives 0.0166, this is the variance!
One problem with the variance is that it is not in the same units as the rest of the data (it is squared). To overcome this, we can take the square root, which gives us a parameter in the same units. This parameter is called standard deviation.
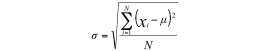
The standard deviation for the data above is 0.1289
Inferential Statistics
Descriptive statistics is solely concerned with properties of the observed data, and does not assume that the data came from a larger population or otherwise. Inferential statistical analysis infers properties about a population from a sample. The whole population is assumed to be larger than the observed sample. Data is obtained using samples because we seldom know the entire population, or it is impractical to obtain this data.
For example, assume that there in fact 200 people in our height example previously, but we have only measured 10. If we are trying to understand the heights of people in the room using the sample data, we are inferring population parameters by using sample data.
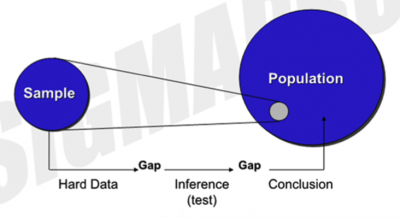
Although the statistical parameters are called the same thing, the symbols and in some cases the formula is different for a population.
|
Parameter |
Sample |
Population |
|
Mean |
µ |
|
|
Standard Deviation |
s |
σ |
|
Proportion |
p |
P |
Population is the totality of the observations with which we are concerned; sample is a subset of observations selected from the population
The Normal Distribution
If we plot 600 observations of aging in accounts receivables we will get a distribution that approaches a curve, but it will still be a little “lumpy” and not a precise curve. If however we plot 6,000 observations we will get a much smoother curve, which appears to be evenly distributed around the mean value.
The resulting curve is called a normal, or Gaussian, distribution. The normal distribution occurs frequently in nature and in organisation processes. A normal distribution will have data points equally distributed around the mean and have a smooth bell shaped curve. The normal distribution is a theoretical concept that is the basis for statistical techniques/tests. A normal distribution is completely described by its mean and standard deviation, the tails of the distribution extend to ± infinity, the area under the curve represents 100% of all possible observations and the curve is symmetrical with 50% of data points each side of the mean.
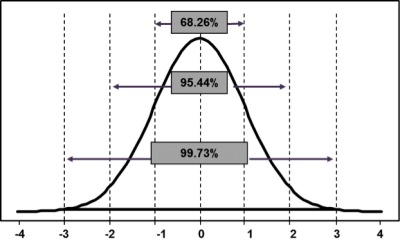
Normality is an assumption behind many statistical tests. Based on our understanding of the normal distribution we can make predictions about the probability of events (such as the probability of a process producing a defect). For any normal distribution, we can calculate the proportion of data points that will fall within a certain range by using the mean and standard deviation.
- 68% of the data points will fall between ± 1 standard deviation
- 95% will fall between ± 2 standard deviations
- 99.7% will fall between ± 3 standard deviations
This empirical rule is extremely useful in calculating performance statistics for processes.
Now consider throwing an (unbiased!) coin with an equal chance of heads or tails. The probability of throwing a head or tail is of course 50:50. What is the chance of throwing 2 heads in a row? Extending the logic, what is the chance of a defect in a process if the previous week’s production there were equal numbers of defects and good production? What is the chance of producing a defect if there were 5 defects out of 100 produced?
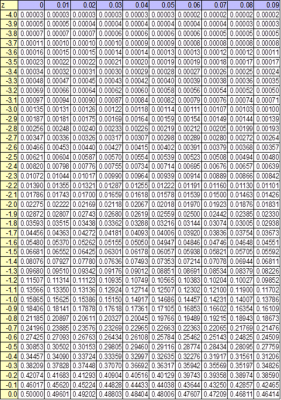
If we know the specification limits, the probability of a defect being produced can be obtained from a Z table which shows the area under the standard normal curve for a particular number of standard deviations.
Categorical Data
Categorical data (or attribute data as it is often called) is where data falls into categories, such as colours (green, red, blue) or days of the week. Categorical data can be used for data such as names, categories, number of defects and so on. In fact any data where items have to be put into “buckets”.
Categorical data includes naming, grading and counting.
It is possible to further subdivide categorical data into two sub-categories:
- Defectives – a defective unit is one which does not meet the specification
- Defects - there are defects on the unit, although that in itself does not make the unit a defective unit! An example would be a car door which has been painted, up to 2 minor defects cold be allowed on the door if they were in inconspicuous areas. So although the door has defects it is not a defective door.
Data for defective units is modelled using the Binomial distribution and data for defects is modelled using Poisson.